Komplexe Zahlen: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „Mit Hilfe der '''komplexen Zahlen''' ist es möglich, Gleichungen wie z.B. <math>x^{2}+1 = 0</math> zu lösen. <br /> Das Einzige, das neu dazukommt, ist die imaginäre Einheit "<math>i</math>", <br /> alle anderen Rechenregeln bleiben erhalten. <br /> == Vorbemerkung und Wiederholung == In der Mittelstufe wurde folgendes gelehrt: <br /> <math>(14 - 5) * (17 - 11) = 9 * 6 = 54</math>. <br /> Oder man rechnet mit doppelter Anwendung des Distributivgese…“ |
Keine Bearbeitungszusammenfassung |
||
| (27 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Mit Hilfe der | __INDEX__ | ||
Mit Hilfe der komplexen Zahlen ist es möglich, Gleichungen wie z.B. <math>x^{2}+1 = 0</math> zu lösen. <br /> | |||
Das Einzige, das neu dazukommt, ist die imaginäre Einheit "<math>i</math>", <br /> | Das Einzige, das neu dazukommt, ist die imaginäre Einheit "<math>i</math>", <br /> | ||
alle anderen Rechenregeln bleiben erhalten. <br /> | alle anderen Rechenregeln bleiben erhalten. <br /> | ||
| Zeile 104: | Zeile 105: | ||
=== Multiplikation === | === Multiplikation === | ||
Nochmals: auch die natürlichen, ganzen, rationalen und reellen Zahlen gehören zu den komplexen Zahlen, ihr Imaginärteil ist Null. <br /><br /> | Nochmals: auch die natürlichen, ganzen, rationalen und reellen Zahlen gehören zu den komplexen Zahlen, ihr Imaginärteil ist Null. <br /><br /> | ||
<math>17 = 17 + 0 | <math>17 = 17 + 0*i</math> <br /><br /> | ||
Beispiel 1 <br /><br /> | Beispiel 1 <br /><br /> | ||
<math> | <math>2 ~ * ~ (6 + 3,5i) = 12 + 7i</math> <br /><br /> | ||
Beispiel 2 <br /><br /> | Beispiel 2 <br /><br /> | ||
<math> | |||
<math>3i ~ * ~ 17i = (3*17*i*i) = -51</math> , das Minuszeichen erscheint wegen <math>i^2=-1</math> <br /><br /> | |||
Beispiel 3 <br /><br /> | Beispiel 3 <br /><br /> | ||
| Zeile 169: | Zeile 171: | ||
Hinweis: <br /> | Hinweis: <br /> | ||
<math>i^4=1 ~ </math> bedeutet nicht, dass <math>i=1 ~ </math> ist. Man | <math>i^4=1 ~ </math> bedeutet nicht, dass <math>i=1 ~ </math> ist. Man kann aber <math>i^4 ~ </math> durch "<math>1</math>" ersetzen. <br /><br /> | ||
"<math>i ~ </math>" ist eine Zahl, die es nicht gibt, ist also "imaginär". <br /><br /> | "<math>i ~ </math>" ist eine Zahl, die es nicht gibt, ist also "imaginär". <br /><br /> | ||
| Zeile 353: | Zeile 355: | ||
== Unterschiedliche Darstellungsformen == | == Unterschiedliche Darstellungsformen == | ||
Für die Darstellung einer komplexen Zahl gibt es mehrere Möglichkeiten: <br /> <br /> | Für die Darstellung einer komplexen Zahl gibt es mehrere Möglichkeiten: <br /> <br /> | ||
<big>'''Algebraische Form:''' </big> <br /> | <big>'''Algebraische Form:''' </big> <br /> | ||
<big><math>z = (a + bi)</math>, als Beispiel <math>(7 - 2i)</math> <br /><br /> </big> | <big><math>z = (a + bi)</math>, </big> | ||
<big>als Beispiel: </big> | |||
<big><math>(7 - 2i)</math> <br /><br /> </big> | |||
<big>'''Polarform:''' </big> <br /> | |||
<big><math>(r ~|~ \varphi)</math>, </big> | |||
<big>als Beispiel (in Grad, Modus "deg" auf dem Taschenrechner):</big> | |||
<big><math>(7,28 ~| ~344°)</math> </big> <br /><br /> | |||
<big>'''Trigonometrische Form:''' </big> <br /> | <big>'''Trigonometrische Form:''' </big> <br /> | ||
<big><math>r*(cos \varphi + i*sin \varphi) </math>, als Beispiel im Bogenmaß <math>\sqrt{53}*(cos(6,005) + i*sin(6,005))</math> </big> <br /><br /> | <big><math>r*(cos \varphi + i*sin \varphi) </math>, </big> | ||
<big>als Beispiel (im Bogenmaß, Modus "rad" auf dem Taschenrechner): </big> | |||
<big><math>\sqrt{53}*(cos(6,005) + i*sin(6,005))</math> </big> <br /><br /> | |||
<big>'''Exponentialform:''' </big> <br /> | <big>'''Exponentialform:''' </big> <br /> | ||
<big><math>r*e^{i*\varphi}</math>, als Beispiel <math>7,28*e^{i*6,005}</math> mit der Eulerschen Zahl <math>e = 2,71828</math > </big> <br /><br /> | <big><math>r*e^{i*\varphi}</math>, </big> | ||
<big>als Beispiel: </big> | |||
<big><math>7,28*e^{i*6,005}</math> (mit der Eulerschen Zahl <math>e = 2,71828...</math>)</big> <br /><br /> | |||
<big>'''Zusammenhang zwischen trigonometrischer Form und Exponentialform:''' </big> <br /> | <big>'''Zusammenhang zwischen trigonometrischer Form und Exponentialform:''' </big> <br /> | ||
<big><math>r*e^{i*\varphi}</math> = <math>r*(cos \varphi + i*sin \varphi) </math>, bei <math>r = 1</math> (r ist der Radius bzw. der Betrag der Zahl) ergibt sich </big> | <big><math>r*e^{i*\varphi}</math> = <math>r*(cos \varphi + i*sin \varphi) </math>,</big> | ||
<big>bei <math>r = 1</math> (r ist der Radius bzw. der Betrag der komplexen Zahl) ergibt sich</big> | |||
<big><math>e^{i*\varphi}</math> = <math>(cos \varphi + i*sin \varphi) </math>, Herleitung folgt später </big> <br /><br /><br /> | <big><math>e^{i*\varphi}</math> = <math>(cos \varphi + i*sin \varphi) </math>, Herleitung folgt später </big> <br /><br /><br /> | ||
| Zeile 369: | Zeile 394: | ||
Wenn die kartesischen Koordinaten einer komplexen Zahl gegeben sind, dann können wir daraus <br /> | Wenn die kartesischen Koordinaten einer komplexen Zahl gegeben sind, dann können wir daraus <br /> | ||
den Betrag (die Länge) und den Winkel zur reellen Achse ermitteln. Wir werden an vier Beispielen <br /> | den Betrag (die Länge) und den Winkel zur reellen Achse ermitteln. Wir werden an vier Beispielen <br /> | ||
den Winkel <math>\varphi</math> errechnen und dazu je nach Lage der Zahl in einem Quadranten <br /> | |||
einen entsprechenden Korrekturwinkel addieren. | |||
Wir rechnen ab jetzt nicht mehr in Grad, sondern im Bogenmaß (rad). Der Taschenrechner muss auf <br /> | Wir rechnen ab jetzt nicht mehr in Grad, sondern im Bogenmaß (rad). Der Taschenrechner muss auf <br /> | ||
rad eingestellt sein! | den Modus "rad" eingestellt sein! | ||
Zur Bestimmung von <math>\varphi</math> nehmen wir zunächst den Tangens, den wir aus <br /> | Zur Bestimmung von <math>\varphi</math> nehmen wir zunächst den Tangens, den wir aus <br /> | ||
Realteil und Imaginärteil berechnen können. <br /> | Realteil und Imaginärteil berechnen können. <br /> | ||
'''Berechnung im 1. Quadranten''' <br /> | |||
<div style="clear: both;"> | |||
<br /><br /> | |||
'''Berechnung im 1. Quadranten''' | |||
<br /><br /> | |||
<math>tan ~ \varphi = \frac{Gegenkathete}{Ankathete}</math> | <math>tan ~ \varphi = \frac{Gegenkathete}{Ankathete}</math> | ||
</div> | |||
<div style="clear: both;"> | <div style="clear: both;"> | ||
<br /> | |||
[[Datei:Komplexe Zahlen Winkel 1Q.png|gerahmt|links|Die komplexe Zahl 4 + 2i im 1. Quadranten]] | [[Datei:Komplexe Zahlen Winkel 1Q.png|gerahmt|links|Die komplexe Zahl 4 + 2i im 1. Quadranten]] | ||
</div> | </div> | ||
<div style="clear: both;"> | <div style="clear: both;"> | ||
<br /><br /> | |||
'''Berechnung im 2. Quadranten''' | '''Berechnung im 2. Quadranten''' | ||
</ | <br /><br /> | ||
<math>tan ~ \alpha = \frac{Gegenkathete}{Ankathete}</math> | <math>tan ~ \alpha = \frac{Gegenkathete}{Ankathete}</math> | ||
</div> | </div> | ||
<div style="clear: both;"> | <div style="clear: both;"> | ||
<br /> | |||
[[Datei:Komplexe Zahlen Winkel 2Q.png|gerahmt|links|Die komplexe Zahl -5 + 3i im 2. Quadranten]] | [[Datei:Komplexe Zahlen Winkel 2Q.png|gerahmt|links|Die komplexe Zahl -5 + 3i im 2. Quadranten]] | ||
</div> | </div> | ||
<div style="clear: both;"> | <div style="clear: both;"> | ||
<br /><br /> | |||
'''Berechnung im 3. Quadranten''' | '''Berechnung im 3. Quadranten''' | ||
<br /><br /> | |||
<math>tan ~ \alpha = \frac{Gegenkathete}{Ankathete}</math> | |||
</div> | </div> | ||
<div style="clear: both;"> | <div style="clear: both;"> | ||
<br /> | |||
[[Datei:Komplexe Zahlen Winkel 3Q.png|gerahmt|links|Die komplexe Zahl -1 - 7i im 3. Quadranten]] | [[Datei:Komplexe Zahlen Winkel 3Q.png|gerahmt|links|Die komplexe Zahl -1 - 7i im 3. Quadranten]] | ||
</div> | </div> | ||
<div style="clear: both;"> | <div style="clear: both;"> | ||
</ | <br /><br /> | ||
< | |||
'''Berechnung im 4. Quadranten''' | '''Berechnung im 4. Quadranten''' | ||
<br /><br /> | |||
<math>tan ~ \alpha = \frac{Gegenkathete}{Ankathete}</math> | |||
</div> | </div> | ||
<div style="clear: both;"> | <div style="clear: both;"> | ||
<br /> | |||
[[Datei:Komplexe Zahlen Winkel 4Q.png|gerahmt|links|Die komplexe Zahl -5 - 5i im 4. Quadranten]] | [[Datei:Komplexe Zahlen Winkel 4Q.png|gerahmt|links|Die komplexe Zahl -5 - 5i im 4. Quadranten]] | ||
</div> | </div> | ||
<div style="clear: both;"> | |||
<br /><br /> | |||
== Rechnen mit komplexen Zahlen in google == | == Rechnen mit komplexen Zahlen in google == | ||
Komplexe Zahlen können auch in Exponenten auftauchen. Damit sich niemand eine Vorstellung von "<math>i</math>" <br /> | Komplexe Zahlen können auch in Exponenten auftauchen. Damit sich niemand eine Vorstellung von "<math>i</math>" <br /> | ||
| Zeile 428: | Zeile 472: | ||
(e hoch (pi*i)) + 1 <br /><br /> | (e hoch (pi*i)) + 1 <br /><br /> | ||
</div> | </div> | ||
== Weblinks == | == Weblinks == | ||
| Zeile 435: | Zeile 481: | ||
* [https://www.youtube.com/watch?v=nzVckYlx3-Y Zeichnerische Multiplikation] | * [https://www.youtube.com/watch?v=nzVckYlx3-Y Zeichnerische Multiplikation] | ||
* [https://www.youtube.com/watch?v=xn3hSozSkyY Gleichungen lösen] | * [https://www.youtube.com/watch?v=xn3hSozSkyY Gleichungen lösen] | ||
[[Kategorie:Seiten, die indexiert werden können]] | |||
Aktuelle Version vom 19. September 2025, 22:31 Uhr
Mit Hilfe der komplexen Zahlen ist es möglich, Gleichungen wie z.B. [math]\displaystyle{ x^{2}+1 = 0 }[/math] zu lösen.
Das Einzige, das neu dazukommt, ist die imaginäre Einheit "[math]\displaystyle{ i }[/math]",
alle anderen Rechenregeln bleiben erhalten.
Vorbemerkung und Wiederholung
In der Mittelstufe wurde folgendes gelehrt:
[math]\displaystyle{ (14 - 5) * (17 - 11) = 9 * 6 = 54 }[/math].
Oder man rechnet mit doppelter Anwendung des Distributivgesetzes:
[math]\displaystyle{ 14*17 - 5*17 -14*11 + 5*11 = 238 - 85 - 154 + 55 = 54. }[/math]
Wir sehen: [math]\displaystyle{ (-5)*(-11) }[/math] muss [math]\displaystyle{ 55 }[/math] ergeben, oder kürzer: "Minus mal Minus ergibt Plus".
Somit ergibt sich: [math]\displaystyle{ (-7)*(-7) = 49 }[/math]
Wäre das nicht so, dann würde das Gefüge von Addition und Multiplikation sofort zusammenbrechen,
weil die Distributivgesetze verletzt wären. Und wir sind auch gewohnt: "Plus mal Plus ergibt Plus".
Das Quadrieren einer Zahl ungleich Null führt also immer zu einer positiven Zahl.
[math]\displaystyle{ i^{2} = -1, }[/math]
Und nun kommt eine Ausnahme, die imaginäre Einheit "[math]\displaystyle{ i }[/math]". Und hier gilt:
[math]\displaystyle{ i*i = -1. }[/math]
Oder anders geschrieben:
[math]\displaystyle{ i^{2} = -1. }[/math]
Reelle Zahlen
Die reellen Zahlen kennen die meisten von uns, Beispiele:
[math]\displaystyle{ -23, }[/math]
[math]\displaystyle{ \sqrt{5}, }[/math]
[math]\displaystyle{ 0, }[/math]
[math]\displaystyle{ 1, }[/math]
[math]\displaystyle{ 114,375, }[/math]
[math]\displaystyle{ log 19. }[/math]
Die Menge der reellen Zahlen wird mit "[math]\displaystyle{ \mathbb{R} }[/math]" bezeichnet.
Imaginäre Zahlen
Neu sind jetzt die imaginären Zahlen:
[math]\displaystyle{ 24*i, }[/math]
[math]\displaystyle{ -9*i, }[/math]
[math]\displaystyle{ \sqrt{2}*i. }[/math]
Die imaginäre Einheit "[math]\displaystyle{ i }[/math]" kann man ebenfalls als imaginäre Zahl bezeichnen.
Die Menge der imaginären Zahlen hat keine eigene Abkürzung.
Komplexe Zahlen
Eine komplexe Zahl entsteht durch Zusammenfügen einer rellen Zahl und einer imaginären Zahl,
das sieht dann so aus:
[math]\displaystyle{ 4 + 7*i. }[/math]
Sie lesen richtig. FÜNF Symbole in einer Zahl: [math]\displaystyle{ 4, +, 7, * }[/math] und das "[math]\displaystyle{ i }[/math]"!
Addition und Multiplikation werden jedoch nicht bzw. nicht in der bisher gewohnten Form durchgeführt.
Diese neu entstandenen Zahlen bilden die Menge der komplexen Zahlen, sie wird mit "[math]\displaystyle{ \mathbb{C} }[/math]" bezeichnet.
Die komplexe Zahl [math]\displaystyle{ 4 + 7*i }[/math] hat den Realteil "4" und den Imaginärteil "7".
Bei einer imaginären Zahl ist der Realteil gleich 0, bei einer reellen Zahl ist der Imaginärteil gleich 0.
WICHTIGE HINWEISE
- "[math]\displaystyle{ i }[/math]" ist keine Variable, wir setzen keine Werte ein, es gilt [math]\displaystyle{ i^{2} = -1. }[/math]
- "[math]\displaystyle{ i }[/math]" ist nicht "irgend etwas mit eins oder Wurzel aus eins" und hat auch nichts mit eins zu tun.
Wir berechnen nicht [math]\displaystyle{ 7*i. }[/math]
- Wir nehmen auch keine Verkürzung vor, indem wir [math]\displaystyle{ 4+7*i }[/math] oder [math]\displaystyle{ 4+7 }[/math] berechnen.
Wenn [math]\displaystyle{ 4+7*i }[/math] das Ergebnis einer Berechnung ist, dann bleibt die Zahl so stehen.
- Realteil UND Imaginärteil einer komplexen Zahl sind reelle Zahlen.
- Die Definition [math]\displaystyle{ i= \sqrt{-1} }[/math] ist zwar richtig, man sollte sie aber trotzdem so nicht hinschreiben.
- Beim Ausdruck [math]\displaystyle{ \sqrt{-16} }[/math] ersetzt man besser das Minuszeichen unter der Wurzel durch [math]\displaystyle{ i^{2} }[/math],
- [math]\displaystyle{ \sqrt{-16} = \sqrt{16*i^{2}} = 4*i. }[/math]
Die Menge der komplexen Zahlen umfasst somit die natürlichen Zahlen, die ganzen Zahlen,
die rationalen Zahlen, die reellen Zahlen, die imaginären Zahlen und die zusammengesetzten,
also "echt komplexen" Zahlen. Man kann also sagen, dass die Menge der komplexen Zahlen
die Menge aller Zahlen ist. Einige Beispiele:
[math]\displaystyle{ 1,275 - 3i, }[/math]
[math]\displaystyle{ \frac{-17}{9} + \sqrt{2}i, }[/math]
[math]\displaystyle{ 5i, }[/math]
[math]\displaystyle{ -23, }[/math]
[math]\displaystyle{ \sqrt{5}, }[/math]
[math]\displaystyle{ 0, }[/math]
[math]\displaystyle{ 1. }[/math]
Google kann sehr gut mit komplexen Zahlen rechnen. Geben Sie einfach mal die Zeichenfolge [math]\displaystyle{ i*i }[/math]
in das google-Suchfeld ein! Oder [math]\displaystyle{ (-i)*(-i). }[/math] Wir kommen noch darauf zurück.
Addition und Subtraktion
Das ist einfach. Wir addieren (oder subtrahieren) die Realteile und imaginären Zahlen getrennt voneinander.
[math]\displaystyle{ (5 + 17i) + (7 + 8i) ~ = ~ 12 + 25i }[/math]
[math]\displaystyle{ (4 + 2i) - (7 - 22i) ~ = ~ -3 + 24i }[/math]
Multiplikation
Nochmals: auch die natürlichen, ganzen, rationalen und reellen Zahlen gehören zu den komplexen Zahlen, ihr Imaginärteil ist Null.
[math]\displaystyle{ 17 = 17 + 0*i }[/math]
Beispiel 1
[math]\displaystyle{ 2 ~ * ~ (6 + 3,5i) = 12 + 7i }[/math]
Beispiel 2
[math]\displaystyle{ 3i ~ * ~ 17i = (3*17*i*i) = -51 }[/math] , das Minuszeichen erscheint wegen [math]\displaystyle{ i^2=-1 }[/math]
Beispiel 3
[math]\displaystyle{ (2 + 7i) * (5 + 9i) }[/math]
[math]\displaystyle{ = 2*5 + 7i*5 + 2*9i + 7i*9i }[/math]
[math]\displaystyle{ = 10 + 35i +18i -63, }[/math]
[math]\displaystyle{ = -53 + 53i }[/math]
Zur Übung seien folgende Berechnungen empfohlen:
[math]\displaystyle{ (2 + 3i) * (4 - 5i) }[/math]
[math]\displaystyle{ (8 + 3i) * (8 - 3i) }[/math] Die dritte binomische Formel taucht hier auf
[math]\displaystyle{ (8 + 3i) * (-8 - 3i) }[/math]
Ihre Ergebnisse lassen sich mit google nachprüfen, dazu sind jeweils
(2 + 3*i) * (4 - 5*i)
(8 + 3*i) * (8 - 3*i)
(8 + 3*i) * (-8 - 3*i)
mit Hilfe von copy + paste in das google-Suchfeld zu übertragen.
Division
Tritt im Nenner ein Imaginärteil auf, dann muss man den Bruch erweitern und zwar
mit der konjugiert komplexen Zahl des Nenners. "Konjugiert" bedeutet, dass das Vorzeichen
des Imaginärteils wechselt. Das sieht so aus:
[math]\displaystyle{ z=23-17i ~ =\gt \overline{z}=23+17i }[/math]
Beispiel für eine Division:
[math]\displaystyle{ \frac{7+4i}{8+9i} }[/math]
Erweitern von Zähler und Nenner mit
[math]\displaystyle{ (8-9i) }[/math]
= [math]\displaystyle{ \frac{(7+4i)(8-9i)}{(8+9i)(8-9i)} }[/math]
= [math]\displaystyle{ \frac{56+32i-63i-36i^2}{64+72i-72i-81i^2} }[/math]
= [math]\displaystyle{ \frac{92-31i}{145} }[/math]
= [math]\displaystyle{ 0,6345-0,2138i }[/math]
Potenzen von i
[math]\displaystyle{ i^0=1 }[/math]
[math]\displaystyle{ i^1=i }[/math]
[math]\displaystyle{ i^2=-1 }[/math]
[math]\displaystyle{ i^3=i^2*i=-i }[/math]
[math]\displaystyle{ i^4=i^2*i^2=1 }[/math]
[math]\displaystyle{ i^5=i }[/math]
[math]\displaystyle{ i^6=-1 }[/math]
[math]\displaystyle{ i^7=-i }[/math]
[math]\displaystyle{ i^8=1 }[/math]
usw.
Hinweis:
[math]\displaystyle{ i^4=1 ~ }[/math] bedeutet nicht, dass [math]\displaystyle{ i=1 ~ }[/math] ist. Man kann aber [math]\displaystyle{ i^4 ~ }[/math] durch "[math]\displaystyle{ 1 }[/math]" ersetzen.
"[math]\displaystyle{ i ~ }[/math]" ist eine Zahl, die es nicht gibt, ist also "imaginär".
Übungsempfehlung: [math]\displaystyle{ z^2 + 2z +3, ~ mit ~ z= -1 + \sqrt{2}*i }[/math]
Wenn Sie es bis hierhin geschafft haben, dann können Sie die Konstruktion der sogenannten
Mandelbrot-Menge verstehen!
Gauß'sche Zahlenebene
Die Gaußsche Zahlenebene ist ein Koordinatensystem mit zwei Achsen,
die senkrecht aufeinanderstehen. Dazu folgende Anmerkungen:
- Die senkrechte Achse (Im) enthält als Markierungen die imaginären Zahlen.
In unseren Beispielen geben wir die Imaginärteile (-2, -1, 0, 1, 2, 3...) an, andere Autoren
schreiben -2i, -i, 0, i, 2i, 3i ... Manchmal werden die Achsen mit x und y statt mit Re und Im
bezeichnet.
- Für das Rechnen mit reellen Zahlen genügt der Zahlenstrahl,
in der komplexen Zahlenebene bewegen wir uns in zwei Dimensionen.
Leider lassen sich Funktionen schlecht darstellen, unter Umständen
benötigen wir zwei Koordinatensysteme.
- Die Multiplikation zweier imaginärer Zahlen führt uns auf die reelle Achse,
umgekehrt passiert das nicht.
- Einen Vergleich zweier komplexer Zahlen durch eine Ordnungsrelation [math]\displaystyle{ z_1 \lt z_2 ~ }[/math] oder [math]\displaystyle{ ~ z_3 \gt z_4 }[/math]
gibt es nicht; wir können nicht feststellen, welche der beiden Zahlen [math]\displaystyle{ 4 + 7*i ~ }[/math] und [math]\displaystyle{ ~ 3 + 8*i }[/math] die größere ist.
Beispiel 1
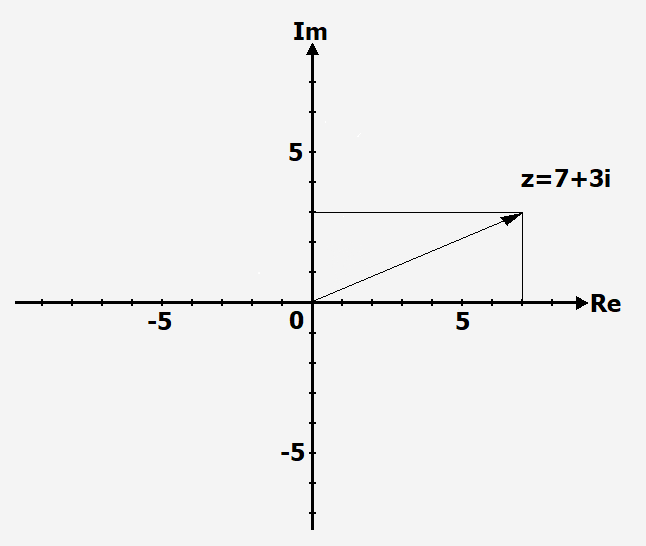
Wir wollen die Zahl [math]\displaystyle{ z=7+3i }[/math] in der Gaußschen Zahlenebene eintragen. Zunächst gehen wir auf der
reellen Achse 7 Längeneinheiten nach rechts und dann parallel zur imaginären Achse 3 Längeneinheiten
nach oben.
Betrag (Länge) einer komplexen Zahl
Der Betrag, also die Länge von [math]\displaystyle{ z=7+3i }[/math] ist:
[math]\displaystyle{ |z|=\sqrt{7^2+3^2}=\sqrt{58} ~ = ~ 7,62... ~ LE }[/math]
LE ist die Abkürzung für Längeneinheiten.
Das "LE" werden wir in Zukunft weglassen, bei einer Multiplikation im Komplexen entstehen
keine Quadratmeter oder Kubikmeter aus Längeneinheiten.
Was wir sehen ist nichts anderes, als der Satz des Pythagoras. [math]\displaystyle{ |z| }[/math] ist die Hypotenuse;
Realteil und Imaginärteil sind die Katheten.
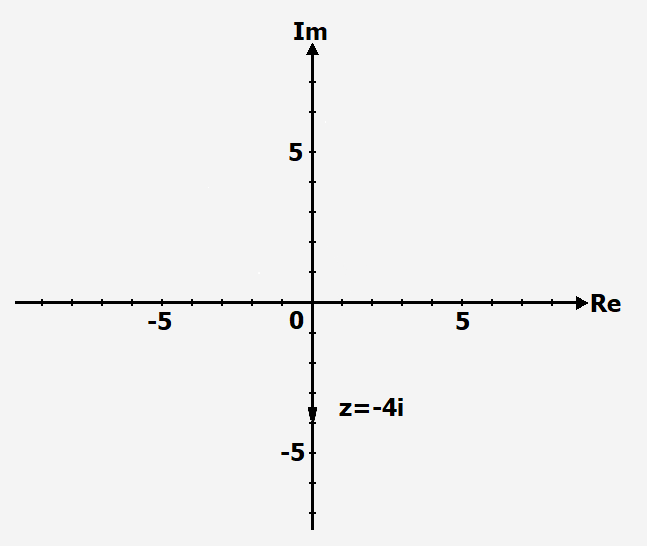
Beispiel 2
Hier ist [math]\displaystyle{ z=-4i }[/math] eingezeichnet. Der Betrag ist [math]\displaystyle{ |z|=4 }[/math] .
Der Betrag einer komplexen Zahl ist stets eine nichtnegative reelle Zahl.
Übungsvorschläge:
Gegeben: [math]\displaystyle{ z=6-7i. }[/math] Wie groß ist [math]\displaystyle{ |z| }[/math]?
Gegeben: [math]\displaystyle{ z=1+i. }[/math] Wie groß ist [math]\displaystyle{ |z|? }[/math] Kleine Hilfe: [math]\displaystyle{ 1+i=1+1i }[/math]
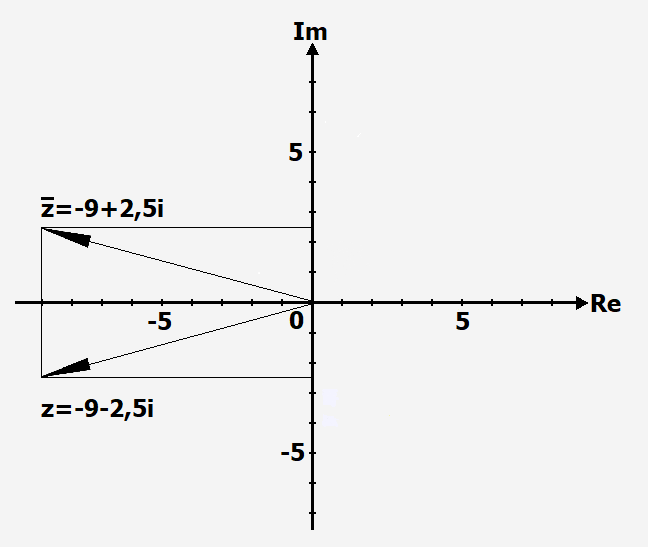
Beispiel 3
Hier haben wir [math]\displaystyle{ z=-9-2,5i ~ }[/math] und die konjugiert komplexe Zahl [math]\displaystyle{ ~ \overline{z}=-9+2,5i }[/math] eingetragen.
Übungsvorschläge: Berechnen Sie [math]\displaystyle{ z+\overline{z} ~, ~ z-\overline{z} ~ }[/math] und [math]\displaystyle{ ~ \overline{z}-z. }[/math]
Zeichnerische Addition
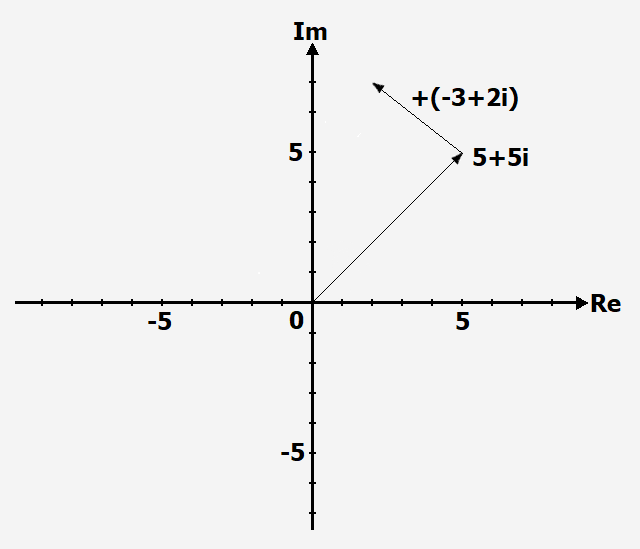
In drei Schritten zeigen wir die Addition der Zahlen [math]\displaystyle{ (5 + 5i) ~ + ~ (-3 + 2i). }[/math]
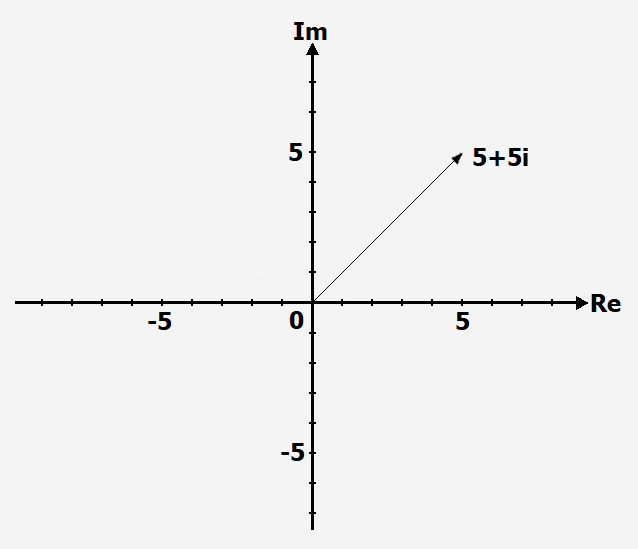
Schritt 1
Den ersten Summanden einzeichnen:
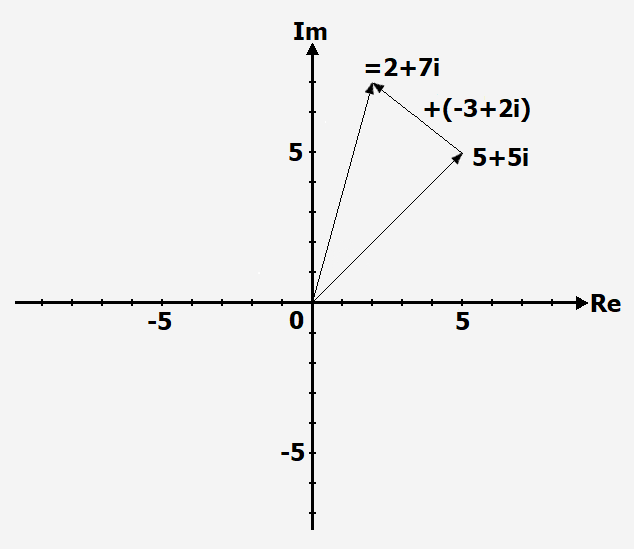
Schritt 2
Die Komponenten des zweiten Summanden an die Pfeilspitze des ersten setzen:
Schritt 3
Die dritte Pfeilspitze zeigt das Ergebnis an:
Zeichnerische Subtraktion
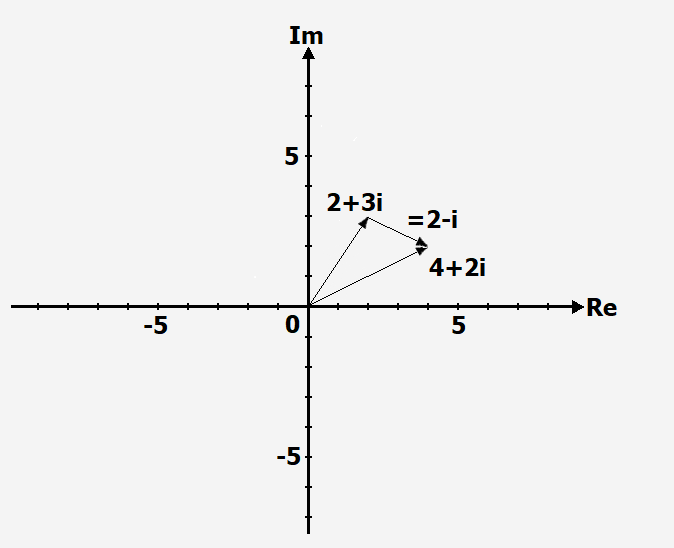
Wir ermitteln die Differenz von [math]\displaystyle{ (4 + 2i) ~ - ~ (2 + 3i). }[/math]
Dazu zeichnen wir beide Zahlen ein. Zunächst durchlaufen wir den Subtrahenden
2+3i in entgegengesetzter Pfeilrichtung (wegen des Minuszeichens) und erreichen
den Ursprung des Koordinatensystems. Nun führen wir eine Addition aus, indem wir
den Minuenden 4+2i im Ursprung anfügen. Die Verbindung von Startpunkt zum Zielpunkt
ergibt die gesuchte Differenz.
Übungsempfehlung: in ein Koordinatensystem ist zu zeichnen
[math]\displaystyle{ (2 + 3i) ~ - ~ (4 + 2i)~ }[/math]
und
[math]\displaystyle{ -(2 + 3i) ~ - ~ (4 + 2i). }[/math]
Wiederholung Trigonometrie
Alles über Winkelfunktionen ist hier als Wiederholung gedacht, wenn etwas zu schnell geht,
dann hilft youtube mit Lehrerschmidt und anderen weiter.
Ein Kreis ist eingeteilt in 2*2*2*3*3*5 = 360 gleich große Teile. Ein Grad ist der 360te Teil eines
Kreises. Ein Viertelkreis beträgt 90° und heißt rechter Winkel.
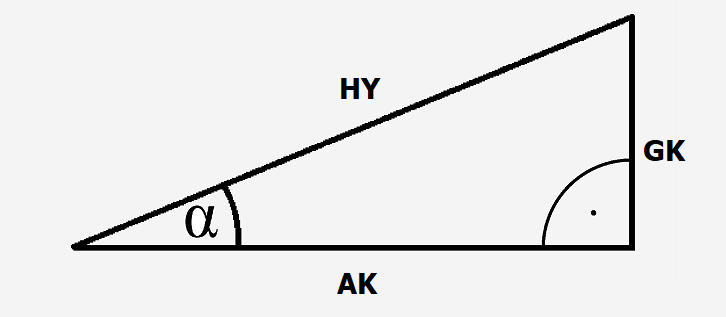
Das folgende Bild zeigt ein rechtwinkliges Dreieck mit dem Winkel [math]\displaystyle{ \alpha }[/math] = 24°.
Daraus lässt sich mit einem Taschenrechner das Verhältnis aus der Gegenkathete von [math]\displaystyle{ \alpha }[/math]
dividiert durch die Hypotenuse ermitteln. Das ist der Sinus des Winkels [math]\displaystyle{ \alpha. }[/math]
Die Eingabe von sin (24°) führt zu dem Ergebnis 0,40673...
Man muss darauf achten, dass der Taschenrechner auf Grad (deg) eingestellt ist.
Das Ergebnis kann man nachprüfen, indem man die Linienlängen von GK und HY
nachmisst und dann dividiert.
Wenn man zusätzlich zum Winkel [math]\displaystyle{ \alpha }[/math] eine weitere Seitenlänge des Dreiecks kennt,
lässt sich das gesamte Dreieck berechnen.
Übungsvorschlag:
Gegeben: Ein rechtwinkliges Dreieck mit [math]\displaystyle{ \alpha }[/math] = 53°, Hypotenuse = 15 cm.
Gesucht: die Länge beider Katheten. Hinweis: Die Winkelsumme eines Dreiecks ist
180°, der andere Winkel [math]\displaystyle{ \beta }[/math] ist damit 90°-53°=37°. Die Gegenkathete des Winkels [math]\displaystyle{ \alpha }[/math]
ist gleichzeitig die Ankathete des Winkels [math]\displaystyle{ \beta. }[/math]
Haben wir umgekehrt das Seitenverhältnis aus Gegekathete:Hypotenuse gegeben, dann können
wir mit Hilfe des Arkussinus den Winkel berechnen. Auf dem Taschenrechner ist das meistens
die Taste [math]\displaystyle{ sin^{-1}. }[/math] Achtung: das ist nicht der Kehrwert, sondern die Umkehrfunktion.
Ferner erhalten wir mit Anwendung des Satzes von Pythagoras [math]\displaystyle{ sin^2 \alpha + cos^2 \alpha = ~1. }[/math]
Eine andere Schreibweise ist [math]\displaystyle{ (sin~\alpha)^2 ~ + ~ (cos~\alpha)^2 = ~1. }[/math]
Übungsvorschlag:
Gegeben ist das Verhältnis GK:HY=0,669106. Wie groß ist der Winkel [math]\displaystyle{ \alpha }[/math]?
Weitere Winkelfunktionen
- Der Kosinus (cos) eines Winkels ist das Verhältnis Ankathete dividiert durch Hypotenuse
- Der Tangens (tan) eines Winkels ist Gegenkathete dividiert durch Ankathete
- Der Kotangens (cot) eines Winkels ist Ankathete dividiert durch Gegenkathete, also der Kehrwert von tan.
Die Begriffe Sekans und Kosekans kommen nur selten vor, es handelt sich -genauso wie Kotangens- um Kehrwerte.
tan (90°) ist nicht definiert.
Umrechnung in das Bogenmaß
Es ist auch eine andere Teilung eines Kreises üblich: das Bogenmaß. Hier nehmen wir
einen Kreis mit dem Radius 1. Wegen der Kreisformel [math]\displaystyle{ U=2r\pi }[/math] ist der Umfang des ganzen
Kreises 2[math]\displaystyle{ \pi }[/math]. Der gestreckte Winkel von 180° ist umgerechnet [math]\displaystyle{ \pi }[/math] und der rechte Winkel
90° ist [math]\displaystyle{ \pi }[/math]/2. Die Zahlen im Bogenmaß sind kleiner, wir haben einen Umrechnungsfaktor von
von 360°/2[math]\displaystyle{ \pi }[/math] = 57,29578... also 1 rad = 57,29578°.
Wichtig: der Taschenrechner muss korrekt eingestellt sein. Bei Grad auf deg (degrees),
beim Bogenmaß auf rad (radiant). Die "Einheit" rad, die eigentlich keine ist, sondern nur Teil
eines Kreises, wird meistens weggelassen. Wir schreiben also entweder [math]\displaystyle{ sin~(\pi/8) }[/math]
oder [math]\displaystyle{ sin~22,5°. }[/math]
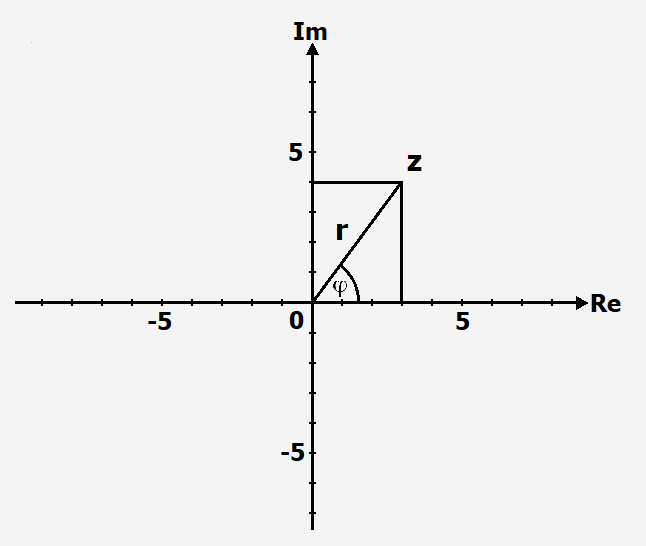
Komplexe Zahlen in Polardarstellung
Eine komplexe Zahl kann man auch dann in ein Koordinatensystem eintragen, wenn man
ihren Betrag, also die Länge kennt und den Winkel zwischen Betrag und der reellen Achse.
Mit der Anwendung des Satzes von Pythagoras sieht die Zahl [math]\displaystyle{ z=3 + 4i }[/math] so aus:
[math]\displaystyle{ z=(5; 53°). }[/math] Der Winkel von 53,13 Grad ergibt sich aus dem Arkustangens von 4:3.
Auf dem Taschenrechner gibt man ein: [math]\displaystyle{ tan^{-1}(4:3) }[/math], ggf. muss auf deg (degrees) umgestellt werden.
In diesem Beispiel sind alle Einheiten der Seitenlängen natürliche Zahlen
(Realteil= 3, Imaginärteil= 4, Radius= 5 oder auch "Maurerdreieck", denn [math]\displaystyle{ 3^2 + 4^2 = 5^2 }[/math])
Allgemein schreibt man [math]\displaystyle{ z=(r; \varphi), }[/math] wobei r=[math]\displaystyle{ |z|. }[/math]
Wir verwenden bei den komplexen Zahlen für den Winkel den griechischen Buchstaben [math]\displaystyle{ \varphi }[/math],
genannt "phi". Mit der Polarform kann man aber nicht rechnen, wir brauchen dazu
die trigonometrische Darstellung oder die Exponentialform. Die Umformungen sind einfach,
aber zeitaufwändig.
Zeichnerische Multiplikation
Zu berechnen ist das Produkt von [math]\displaystyle{ (2 + i) ~ * ~ (2 + 6i). }[/math]
Man addiert die Winkel der beiden Faktoren, den sie jeweils mit der positiven reellen Achse bilden.
Dann hat man zunächst "die Richtung des Produkts". Als nächstes multipliziert man die Beträge
beider Zahlen und erhält den Betrag als Länge. Diese Länge ist dann vom Ursprung abzutragen.
Das komplette Verfahren kann man sich auf youtube ansehen, das uns von
Prof. Jörn Loviscach vorgestellt wird.
Übungsvorschlag: Zeichnen Sie [math]\displaystyle{ (4 + 7i) ~ * ~ i~. }[/math]
Unterschiedliche Darstellungsformen
Für die Darstellung einer komplexen Zahl gibt es mehrere Möglichkeiten:
Algebraische Form:
[math]\displaystyle{ z = (a + bi) }[/math],
als Beispiel:
[math]\displaystyle{ (7 - 2i) }[/math]
Polarform:
[math]\displaystyle{ (r ~|~ \varphi) }[/math],
als Beispiel (in Grad, Modus "deg" auf dem Taschenrechner):
[math]\displaystyle{ (7,28 ~| ~344°) }[/math]
Trigonometrische Form:
[math]\displaystyle{ r*(cos \varphi + i*sin \varphi) }[/math],
als Beispiel (im Bogenmaß, Modus "rad" auf dem Taschenrechner):
[math]\displaystyle{ \sqrt{53}*(cos(6,005) + i*sin(6,005)) }[/math]
Exponentialform:
[math]\displaystyle{ r*e^{i*\varphi} }[/math],
als Beispiel:
[math]\displaystyle{ 7,28*e^{i*6,005} }[/math] (mit der Eulerschen Zahl [math]\displaystyle{ e = 2,71828... }[/math])
Zusammenhang zwischen trigonometrischer Form und Exponentialform:
[math]\displaystyle{ r*e^{i*\varphi} }[/math] = [math]\displaystyle{ r*(cos \varphi + i*sin \varphi) }[/math],
bei [math]\displaystyle{ r = 1 }[/math] (r ist der Radius bzw. der Betrag der komplexen Zahl) ergibt sich
[math]\displaystyle{ e^{i*\varphi} }[/math] = [math]\displaystyle{ (cos \varphi + i*sin \varphi) }[/math], Herleitung folgt später
Umwandlung verschiedener Darstellungsformen
Wenn die kartesischen Koordinaten einer komplexen Zahl gegeben sind, dann können wir daraus
den Betrag (die Länge) und den Winkel zur reellen Achse ermitteln. Wir werden an vier Beispielen
den Winkel [math]\displaystyle{ \varphi }[/math] errechnen und dazu je nach Lage der Zahl in einem Quadranten
einen entsprechenden Korrekturwinkel addieren.
Wir rechnen ab jetzt nicht mehr in Grad, sondern im Bogenmaß (rad). Der Taschenrechner muss auf
den Modus "rad" eingestellt sein!
Zur Bestimmung von [math]\displaystyle{ \varphi }[/math] nehmen wir zunächst den Tangens, den wir aus
Realteil und Imaginärteil berechnen können.
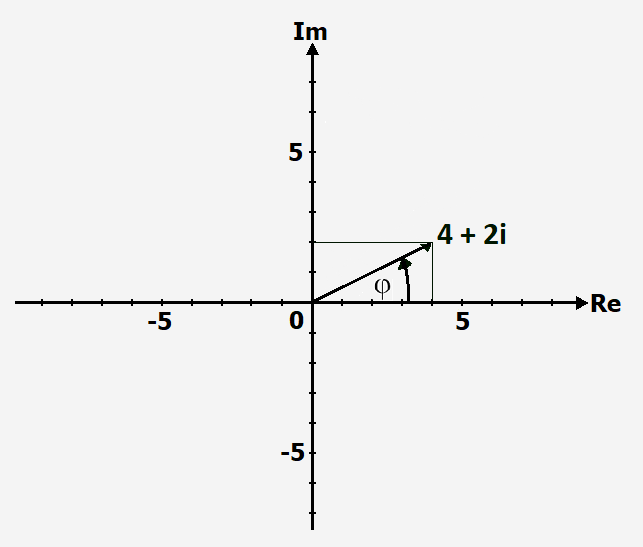
Berechnung im 1. Quadranten
[math]\displaystyle{ tan ~ \varphi = \frac{Gegenkathete}{Ankathete} }[/math]
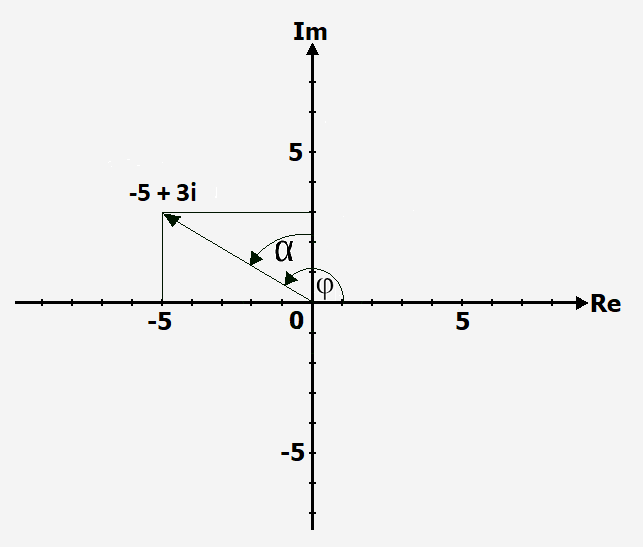
Berechnung im 2. Quadranten
[math]\displaystyle{ tan ~ \alpha = \frac{Gegenkathete}{Ankathete} }[/math]
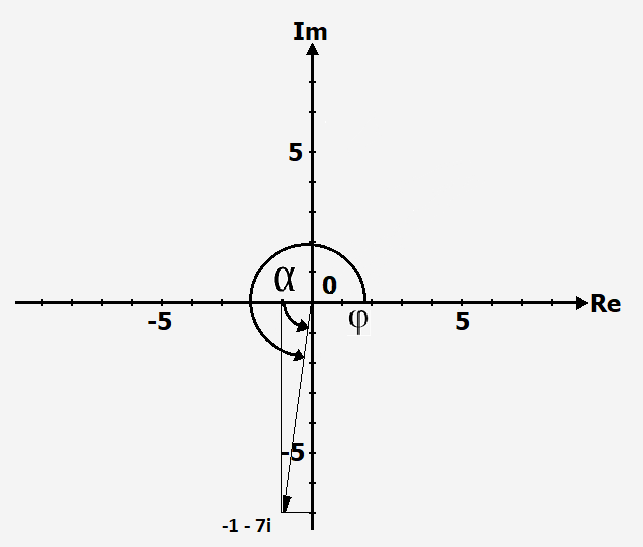
Berechnung im 3. Quadranten
[math]\displaystyle{ tan ~ \alpha = \frac{Gegenkathete}{Ankathete} }[/math]
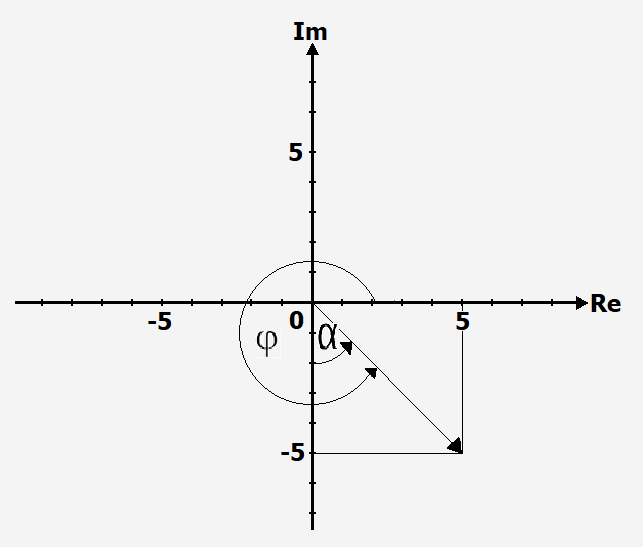
Berechnung im 4. Quadranten
[math]\displaystyle{ tan ~ \alpha = \frac{Gegenkathete}{Ankathete} }[/math]
Rechnen mit komplexen Zahlen in google
Komplexe Zahlen können auch in Exponenten auftauchen. Damit sich niemand eine Vorstellung von "[math]\displaystyle{ i }[/math]"
macht, empfehlen wir folgende Berechnungen mit google, dabei gibt man die Operationen direkt
in das google-Suchfeld ein oder kopiert mit copy + paste. In den folgenden Beispielen
ist der Realteil im Exponenten gleich Null.
2 hoch (3*i) oder 2 ** (3*i) oder 2 to the power (3*i)
2 hoch (7*i)
100 hoch (6*i)
1000 hoch (26*i)
100000 hoch (9000*i)
Zu sehen ist, dass Realteil und Imaginärteil stets zwischen -1 und +1 liegen.
Und nun kommen wir zu der schönsten Formel der Mathematik, das ist die Eulersche Identität:
[math]\displaystyle{ e^{\pi*i} +1 = 0 }[/math]
Für die Eingabe in das google-Suchfeld:
(2,71828183 hoch (3,14159265*i)) +1
oder auch -diesmal ohne Rundungsfehler-
(e hoch (pi*i)) + 1